Recently, I’m reading The Isaac Newton School of Driving.
At the end of Chapter 1, the author mentioned a formula for weight transfer during brake. The derivation is a little bit vague, so I tried to figure out more details.
One more reference: Bilibili video.
I drew the following sketch:
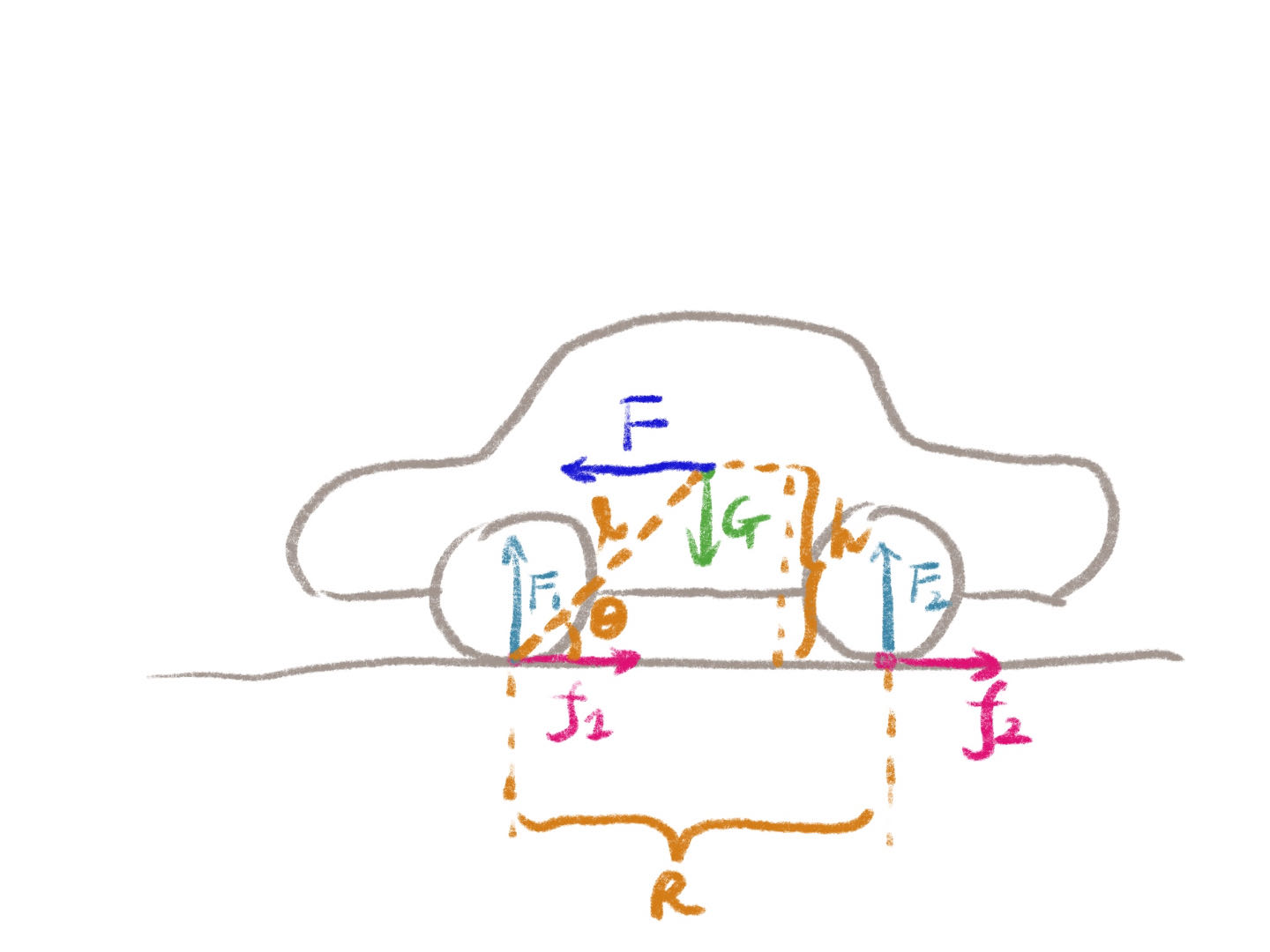
When braking, inertia force $F$ and upwards force $F_2$ at the back axle tend to rotate the car counter-clockwise. The gravity $G$ tends to rotate the car clockwise. The rotation center is the point where front axle meets the ground.
But the car is not rotating, then by equaling the torques, we have \begin{equation*} F\cdot\ell\sin\theta+F_2\cdot R=G\cdot\ell\cos\theta \end{equation*} We can assume the center of mass is exactly at the middle point of the wheelbase, i.e. $\ell\cos\theta=\frac{1}{2}R$. Then we have \begin{equation*} F\cdot h+F_2\cdot R=\frac{1}{2}G\cdot R \end{equation*} \begin{equation*} \iff F\cdot h=(\frac{1}{2}G-F_2)\cdot R \end{equation*}
Notice that when the car is still or moving at constant speed, the upwards force at back axle is $\frac{1}{2}G$, in other words, the weight transfer is $\frac{1}{2}G-F_2$ (reduction of upwards force on back axle). Therefore we have \begin{equation*} W_d=\frac{F\cdot h}{R} \end{equation*} This is the formula in the book.